تفعيل دور الثقافة الشعبية في تدريس الرياضيات للأطفال
العدد 37 - آفاق

“إذا ضللت طريقك فلا تركض نحو الأمام بل عد إلى الوراء حتى تبلغ مكانًا تعرفه” (مثل إفريقي)
لقد تفطن علماء الرياضيات عبر العالم منذ نحو نصف قرن إلى أن تدريس هذه المادة للتلاميذ يعرف تعثرات كثيرة ومتزايدة، وأن الأطفال صاروا ينفرون منها لبعدها عن واقعهم اليومي. وظهرت خلال العقود الأخيرة دراسات دسمة ومتنوعة تسعى كلها إلى إيجاد أحسن السبل لتحسين صورة الرياضيات لدى التلميذ وتبسيط مهمته في إدراك المفاهيم الرياضية دون «التضحية» بالجانب النظري الذي ينمي الفكر والإدراك لدى المتعلم.
ولذلك كانت اليونسكو قد أعلنت سنة 2000 «السنة العالمية للرياضيات» ودعت إلى تنظيم التظاهرات العلمية التي من شأنها تقليص الهوة بين الرياضيات وثقافة المواطن. وفي هذا السياق أقيمت خلال تلك السنة أزيد من 700 مؤتمر وملتقى عبر العالم تدارست كلها كيفيات تقريب الرياضيات من المواطن وتحبيبها للتلميذ. ولا زالت المساعي في هذا الموضوع جارية على قدم وساق إلى اليوم بدون انقطاع. وكان آخر مؤتمر عالمي ضخم حول هذا المحور قد أقيم في جامعة هامبورغ (ألمانيا) من 24 إلى 31 يوليو 2016 حضره أكثر من ثلاثة آلاف باحث في تدريس الرياضيات أتوا من كل بقاع العالم.
وهكذا راح باحثون يتدارسون إمكانية توظيف الإثنورياضيات ethnomathematics في المناهج الدراسية في البلدان الغربية ضمن هذا المسعى التعليمي. أما توظيفها في المجتمعات القبلية وبلدان العالم الثالث فكان بالنسبة إليهم من تحصيل الحاصل. ذلك أن الخبراء يرون أن كل مجتمع ينشئ طرقا ذهنية وفكرية ويدوية خاصة تنبثق من الثقافة الشعبية السائدة فيه؛ ومن شأن هذه الطرق أن توضح إجراء العمليات الحسابية، وكذا إجراء القياسات ورسم الأشكال المختلفة، إلخ. سنسلط الضوء فيما يلي على وضع الإثنورياضيات في العالم وبوجه خاص في بعض البلدان الإفريقية (انظر المرجع (4)).
ما هي الإثنورياضيات؟
يمكن أن نعرف الإثنورياضيات بأنها الأنثروبولوجيا الثقافية للرياضيات وتدريسها، أي أنها دراسة الممارسات والأفكار الرياضية في علاقاتها مع مكونات الحياة الثقافية والاجتماعية. أما الفائدة منها فيراها المختصون - فضلا عن كونها تمثل ثقافة شعبية أصيلة ينبغي العناية بها - بأنها تساعد على تقريب المفاهيم الرياضية والعلمية للتلميذ في المدرسة إذا ما كُيفت بالشكل المناسب مع المناهج المدرسية.
والواقع أن الحديث عن الإثنورياضيات ظهر باحتشام في السبعينيات من القرن الماضي عندما أدخل هذا المصطلح عالم الرياضيات الرائد البرازيلي أبيرتان دامبروزيو Ubiratan D’Ambrosio. لكنه ما لبث أن تكثف النقاش حوله في نهاية الثمانينيات، لا سيما في المؤتمر العالمي لتدريس الرياضيات الذي نظم في بودابست عام 1988 حيث خصص في هذا المؤتمر محورٌ بعنوان «ماذا يمكن أن ننتظر من الإثنورياضيات؟» وقد شارك في تنشيط هذا المحور العديد من العلماء أتوا من الولايات المتحدة والبرازيل وموزنبيق وفلسطين وبريطانيا.
كما أدى البرازيلي إدواردو فريريا Eduardo Ferreira دورا هاما في دراسة النشاطات في الموروث الرياضي لدى الهنود الحمر في البرازيل خلال الثمانينيات. وكان فريريا قد عرّف الإثنورياضيات على أنها «الرياضيات المدمجة في الثقافة الشعبية» (انظر المرجع (5)). بينما يرى الأستاذ مارسيلو بوربا Marcelo Borba الذي درس المعارف الرياضية في حي شعبي برازيلي أن الإثنورياضيات هي الرياضيات التي تمارسها التجمعات الثقافية الشعبية مثل المجتمعات القبلية. ويراها تمثل حقل معارف مرتبطا ارتباطا وثيقا بالثقافة الشعبية ويتم التعبير عنها بلغة من صنع الثقافة الشعبية أيضا، وغالبا ما تختلف عن لغة الرياضيات كعلم قائم بذاته بالشكل الذي نعرفه اليوم في كتبنا المدرسية (انظر المرجع(3)).
من الواضح أن كل هذه التعاريف تصب في نفس الاتجاه وأننا نستطيع اعتبار الإثنورياضيات في آن واحد كفرع من فروع الرياضيات وكفرع من علم الإثنولوجيا (علم الأعراق) المتفرع بدوره عن الأنثربولوجيا (علم الأجناس). كما أنها تُعتبر جزءا لا يتجزأ من تعليمية الرياضيات. وفي هذا السياق يوضح دامبروزيو (انظر المرجع (6)) أن مصطلح «الإثنورياضيات» يعبر عن العلاقة بين الثقافة والرياضيات. وهو يتطلب في كل مرة تفسيرا مرتبطا بالزمان والمكان لأنه يصف مفاهيم مرنة. فكلمة «إثنو» تشير إلى «كل العوامل التي تتشكل منها الهوية الثقافية للمجتمع : اللغة والرموز والقيم والدارج من الكلام والمعتقدات والمأكل والملبس والعادات والملامح الجسدية». أما «الرياضيات» فتشير إلى نظرة واسعة للرياضيات تشمل الحساب والهندسة والترتيب والتصنيف والتداخل والنمذجة، إلخ.
تسمح الإثنورياضيات، حسب دامبروزيو، بإدراك كيف تواصل الرياضيات تكيّفها ثقافيا وكيف تم استعمالها في مختلف الأماكن والعصور. وقد جرت العادة في المدرسة الحديثة على تجاهل البعد الثقافي في تدريس الرياضيات. ومن ثم ساد الاعتقاد لدى الكثيرين بأن لا علاقة تربط الرياضيات بالثقافة! وتتجلى هذه النظرة في طريقة التدريس على أكثر من صعيد : في الغالب يمنع المعلم التلميذ من إنشاء إدراك وفهم شخصي للمفاهيم الرياضية المقدمة في الفصل. كما يتم تجاهل القيم والتقاليد والمعتقدات والعادات الشعبية واللغة التي تعكس الجانب الثقافي خلال الدرس. وهذا يؤثر بدون شك بصفة سلبية على تحصيل التلميذ.
ويلاحظ المختصون في الإثنورياضيات أن التلاميذ يحفظون أسماء لامعة في الرياضيات، مثل الإغريقييْن فيثاغورس وطالس، لكنهم لا يعلمون أن هؤلاء سافروا إلى بلدان قريبة وبعيدة ونهلوا من علوم غيرهم، مثل علوم الهنود والبابليين وقدماء المصريين، إلخ. ومن ثم لا يدرك التلاميذ بأن العديد من الثقافات، ومنها الثقافات الشعبية، قد أسهمت في تطوير الرياضيات وجعلتها اليوم أكثر إبداعا. كما لا يرى هؤلاء التلاميذ أن الرياضيات تشكل، شأنها في ذلك شأن سائر العلوم، تراكما لاكتشافات تمت عبر العصور وفي أوساط ثقافية مختلفة في بقاع العالم، مما يجعل منها فسيفساء من الاسهامات الثقافية المتنوعة المشارب.
والواقع أن هذا الاهتمام بالإثنورياضيات بدأ حديثا في أوروبا الغربية علما أن الولايات المتحدة الأمريكية سبقتها لاهتمامها بالأقليات الإثنية عندها التي جاءت من آسيا وإفريقيا وأمريكا اللاتينية إضافة إلى الهنود الحمر. وقد ظلت الكثير من الكتابات حول هذا الموضوع في بلدان مختلفة، لا سيما البرازيل والمستعمرات القديمة، تكتفي بسرد المشاكل المطروحة والتنديد بعدم مراعاة خصوصيات الثقافة الشعبية في هذه المجتمعات.
وتجدر الملاحظة أننا نجد عددا من خبراء طرق تدريس الرياضيات في البلدان الغربية المتقدمة متخوفين من إدراج عناصر الرياضيات السائدة في الثقافات الشعبية داخل بلدان العالم الثالث في مناهجهم الدراسية الغربية. وهذا التخوف ناجم من كون هؤلاء الخبراء غير قادرين على تصور مدى تداعيات الحديث أمام التلاميذ عن الإثنورياضيات المرتبطة بثقافات شعبية آتية من بعيد. فقد تسيء في نظرهم إلى الفكر العلمي للتلميذ في آخر المطاف! كما أنهم يخشون التداعيات الإيديولوجية والسياسية على المجتمع الغربي الذي صار مجتمعا يجمع العديد من الأجناس والأعراق.
وعلى كل حال فمن مهام الإثنورياضيين القيام بتحليل تأثيرات العوامل الثقافية والاجتماعية على عملية التعلم وتطور الرياضيات. كما يحاولون الإسهام في المعارف الرياضية المكتسبة لدى الشعوب (لا سيما تلك التي كانت مستعمرة) من خلال البحث عن العناصر الثقافية التي لا زالت جلية في الثقافة الشعبية السائدة. وتسعى الدراسات الإثنورياضية في العالم الثالث، على وجه الخصوص، إلى الاهتمام بالتقاليد ذات الصلة بحقل الرياضيات التي صمدت في العهد الاستعماري، ثم محاولة دمجها في المناهج الدراسية. ويلاحظ الخبراء أن ذلك يفتح أيضا أبوابا جديدة أمام تدريس الفلسفة ونشاطات أخرى في هذه البلدان. ومن ثمّ يجد التلميذ انسجاما بين ثقافته المحلية ومحيطه العائلي وما يتعلمه في المدرسة. وهو ما يزيده اعتزازا بما تتميز به الثقافة الشعبية التي ينتسب إليها في مجتمعه وموطنه.
أما علماء الاجتماع فيرون أن الهوية الثقافية للمجتمع هي مصدر إلهام للجهود التي تبذل في سبيل التطور. ولذا فمن الأحسن أن يتلقى التلميذ تربية بكل مركباتها مستغلة عناصر الثقافة المحلية بوجه خاص. وفي هذا الإطار لا بد أن ينظر التلميذ إلى العلوم والرياضيات بأنها وسيلة تتيح له إمكانية فهم ثقافة الوسط الذي يعيش فيه، وأنها أداة تخدم تقدم تلك الثقافة. ومن هذا المنظور فإن الإثنورياضيات تؤدي هذا الدور بامتياز.
والظاهر أن ما دعم الاهتمام بالأثنورياضيات في البداية هو توجه فئة من الأكاديميين تميل إلى تحرير الشعوب والاعتراف بثقافاتها الشعبية وتؤمن بضرورة ترقية كل ما يدعم الهوية القومية. وهذه الفئة هي التي نادت مثلا بترقية الرياضيات الاجتماعية في إفريقيا، أي ترقية تطبيقاتها في حياة الشعوب الإفريقية. وقد أكد هؤلاء الأكاديميون بخصوص الرياضيات الشفوية أن في كل الثقافات الإنسانية هناك معارف رياضية تنتقل شفويا من جيل إلى جيل (انظر المرجع (9)). وهو ما يدعو إلى المزيد من الاهتمام بالإثنورياضيات.
الإثنورياضيات في بوركينا فاسو
يعتبر خليفة طراوري (انظر المرجع (15)) أول مختص في الإثنورياضيات في بوركينا فاسو. وقد نال شهادة الدكتوراه في هذا الاختصاص من جامعة كويبك بمونتريال الكندية عام 2006 بدراسة إثنورياضية لبعض مناطق بوركينا فاسو.
أجرى طراوري دراسته الميدانية في منطقة سيامو Siamou في بوركينا فاسو حيث اهتم بالثقافة والتقاليد الشعبية في مجال الحساب. وتُعرف المنطقة بسكانها الذين هم من صغار المزارعين الأميين والرعاة. وقد حرص طراوري على الإلمام بالطرق التي تطورت من خلال تلك التقاليد في الحساب باعتبار أن الرياضيات عموما ليست أ + ب أو س ، ع ، ص بل تمثل أيضا عنصرا قويا من العناصر المكونة للثقافة الشعبية.
ومن المعروف أنك إذا طرحت السؤال: ما الفائدة من الرياضيات بصيغتها الحالية؟ فإنك لن تحصل على جواب شاف إذا لم تكن ملما بمواضيعها إلا قليلا. ذلك أنك لا تستطيع عندئذ أن تدرك كيف أنها تدخل في حركة السيارة والقطار والطائرة وتصميمها وصناعتها، إلخ. وبطبيعة الحال فمستعملو الرياضيات، مثل الفيزيائيين والمهندسين والكيميائيين، لا يطرحون مثل هذا السؤال. والسائل عموما هو ممن لهم توجه يميل إلى الثقافة العامة والعلوم الإنسانية لأنهم يهتمون بتأثير الرياضيات من الناحية الاجتماعية وتغلغلها في الثقافة الشعبية.
يشير طراوري بهذا الخصوص إلى أن مواجهة هذه الصعوبة جعلت بعض المختصين في الإثنورياضيات يقترحون تعريف الرياضيات على أنها أداة «عمل وتجربة»، بمعنى أنها ممارسة. وعلى ضوء ذلك يقول هؤلاء الباحثون أن الرياضيات تتكون من عدة مجالات منها: العد، وأخذ القياسات، وتحديد المواقع، والتوجيه. ويضيفون أنك إذا كنت تقوم بواحدة منها فأنت تمارس الرياضيات. من الواضح أن الرياضيات إذا ما نظرنا إليها من هذه الزاوية فلن تصبح تلك الرياضيات المبنية على منطق كوني صالح في كل مكان وزمان، بل ستكون رياضيات خاضعة لخصوصيات ثقافية مرتبطة بالبيئة التي يقيم فيها المستخدم (انظر المرجع (16))!
عندما تجد في السوق الشعبية شخصا يبيع فاكهة بسعر 100 د. لثلاث تفاحات مثلا وطلبت أنت تفاحة واحدة فسوف يكون الرد بدون شك : «نحن لا نبيع بالتفاحة الواحدة». يقول طراوري عن هذا الموقف أننا نستنتج منه بسذاجة بأن البائع جاهل لا يتقن الحساب. لكن الواقع يبيّن أن هناك حسابات يقوم بها البائع الشعبي نحن لا نفقهها.
وبهذا الصدد يقول رائد الإثنورياضيات دامبروزيو إن مصادر المعرفة في المجتمعات متنوعة ومتشعبة، وهو ما يجعل كل مجتمع يتميز بتنظيم خاص وبثقافة أصيلة. ولذا علينا ألا نعتقد بأن هذا التنظيم كوني لا يخضع للمكان أو الزمان. على سبيل المثال، إذا كان هناك مبلغ من النقود وطُلب منا تحديد قيمته فسنلاحظ أن كل مجتمع يحددها بطريقة قد تختلف عن طرق الغير. يمكن مثلا أن تكون الطريقة المتبعة مرتبطة بنوع القطع النقدية. مثال آخر كثيرا ما نتفاجأ به : إذا اشتريت 7 قطع حلوى كل منها ب 4 د. فأنت كمتعلم ستقول إن ثمنها هو جداء 7 في 4، أي 28د لأنك تحفظ جدول الضرب وألِفت استعماله. أما الباعة الأميون فمنهم من يحفظ في ذهنه (ككتلة واحدة) أن ثمن 5 قطع هو 20د وأن القطعتين ب 8د وعليه فالمجموع هو 20 + 8 = 28د. الناس يعتبرون عموما أن ثمة علاقات رياضية ينبغي تعلمها واستعمالها وهي صالحة للجميع. والدليل على عدم صحة هذا القول أن هناك من الأطفال من يعرف تلك العلاقات ولا يستطيع تطبيقها.
لاحظ طراوري خلال دراسته، وهذا شيء موجود في أماكن كثيرة، أن في بلدة يقطنها مزارعون صغار في بوركينا فاسو كان الفلاحون يبيعون منتجاتهم ليس بالوزن بل بعدد الحبات. وكان فلاح يبيع كومة من ثمر المانجا (بكمية تقارب ثلاثة أطنان) بسعر 25 فرنك إفريقي لكل سبع حبات. يقول الباحث أننا عندما نتمعن في سلوكات الباعة نكتشف أن هناك طريقة شعبية في إجراء الحسابات تختلف عن القواعد المتداولة لدى من تعلموا الرياضيات في المدارس.
تذكر أيضا التقنية الشعبية التي تتمثل (عندما نريد إقامة زاوية قائمة) في إنشاء مثلث بقضبان خشبية مثلا طول أضلاعه 3 و 4 و 5 وحدات طول (سنتمتر أو متر...). وعندئذ تكون الزاوية بين الضلعين اللذين يبلغ طولاهما 3 و 4 زاويةً قائمةً. وهذا في الواقع يعتبر حالة خاصة من نظرية فيثاغورس. وهذه الطرق لا نجدها في الثقافة الشعبية في قرى بوركينا فاسو فحسب فهي تمتد جغرافيا إلى موزنبيق (كما سنرى أدناه) وإلى مصر القديمة. يقول طراوري إنه سأل أحد الخبراء في الرياضيات حول بعض المسائل التي يحلها فلاحو بوركينا فاسو بطريقتهم في 5 دقائق فتفاجأ عندما لاحظ أن الخبير قضى أكثر من ساعة في البحث عن الجواب الصحيح.
أما في مجال الهندسة فهؤلاء الفلاحون لا يتكلمون عن متوازي الأضلاع والزاوية والقطر وما إلى ذلك من المصطلحات الهندسية، لكنهم يستخدمونها بالشكل الذي تحتاجه أعمالهم. لكن، هل بالإمكان استعمال هذه الفنيات الشعبية في تدريس الرياضيات داخل المدرسة؟ من الواضح أن بعضها يصعب تطبيقها بينما يمكن أن يلم بها المعلم وذلك يسمح له بتحسين أدائه خلال الدرس وإدراك نوع الصعوبات التي يواجهها التلميذ، وهو ما يزيل التخوف النفسي من الرياضيات لدى الطفل وأوليائه. لا شك في أن الصعوبات التي يواجهها التلميذ مرتبطة بثقافته الشعبية السائدة في منطقته. وقد لوحظ ذلك في إفريقيا وحتى لدى الأسكيمو في شمال كندا. وكثيرا ما يتفاجأ المربون عندما يلجأ أحد التلاميذ إلى ثقافته المحلية في تلك المناطق لتبرير عمليات رياضية بحدوث تناقضات في ذهن التلميذ مع ما يتعلمه في المدرسة. ولذا نجد أحيانا التلاميذ تائهين عندما يقومون ببعض العمليات الحسابية.
يذهب طراوري في دراسته إلى تبرير الفشل الدراسي لكثير من تلاميذ المدارس بالسياق الاجتماعي والثقافي الذي يعيشه التلميذ وعدم انسجامه مع المحيط الذي تفرضه المدرسة ومناهجها: يمكن أن تضع نفس التلميذ في وضعيتين ثقافيتين مختلفتين فينجح في إحداها ويفشل في الأخرى.
وفيما يخص الجانب اللغوي فالظاهر أن الثقافة الشعبية التي تنتشر من خلالها خصوصيات اللغة الأم تؤثر كثيرا في التحصيل الدراسي. لكنه يبدو أن علماء اللسانيات لم يحيطوا بعد بكل جوانب هذا الموضوع وقياس مدى التأثير. ومن بين ما يؤثر في الأوساط الشعبية ذات اللهجات المحلية أن الكثير من المفردات التي تستعمل في المدرسة لا توجد في تلك اللهجات. وهو ما ينجرّ عنه الكثير من الغموض في ذهن التلميذ. والأمر قد يتعلق بمصطلح بسيط جدا نحتاجه يوميا، مثال ذلك: لا بد أن نجد في اللغة التي نخاطب بها التلميذ ما يفرق بين الدائرة (وهي المنحنى الدائري المعروف بصفته شكلا هندسيا يبعد بنفس المسافة عن نقطة معلومة، هي المركز) وبين محيط الدائرة (الذي يمثل طول المنحنى الدائري بوحدة السنتمتر أو المتر...) وبين القرص (الذي يمثل الدائرة المملوءة، أي مجموعة كل النقاط الموجودة داخل الدائرة). والأمر كذلك في موضوع الصفر التي تنظر إليه كثير من الثقافات الشعبية على أنه يمثل «لا شيء» أو «العدم» بينما يمثل في الرياضيات شيئا آخر عدا في بعض الحالات.
في أنغولا ومدغشقر...
يحاول الباحثون في الإثنوغرافيا أن يصفوا الطرق المستعملة في الميدان للنفوذ إلى الآليات الذهنية التي تستند إليها الرياضيات وخواصها في الذاكرة الجماعية عند بعض المجتمعات، سيما تلك التي تعتمد على التعبير الشفوي. ومن بين ما يعبر عن الثقافة الشعبية في كثير من بقاع العالم الرسم على الحجارة والصخور والرمال. وهذه الأشكال المرسومة لها طابع هندسي متميز تهتم به الإثنورياضيات وتدرس معالمه وخصوصياته وتربطه بتقاليد وثقافة المواطن البدائية في تلك الأوطان من القارات الخمس.
فإذا نظرنا إلى الرسم على الرمال في موزنبيق نجد في الكثير من الأحيان خطوطا مستمرة ترسم دون رفع الإصبع وتتميز بأنها تُخَط مرة واحدة ولا يعود صاحبها إلى الرسم فوقها مرة ثانية. يلاحظ الباحثون أن لمثل هذه الخطوط خصوصيات رياضية تندرج ضمن نظرية البيانات. وكانت محل دراسة إثنورياضية عام 1998 من قبل مارسيا آشرMarcia Ascher في جمهورية فانواتو Vanuatu الواقعة في جنوب غرب المحيط الهادي وكذلك من قِبل باولس جرديس Paulus Gerdes عام 1995 في أنغولا (إفريقيا). والواقع أن هذه الخطوط ليست خطوطا عفوية بل معبرة عن تقاليد ومعتقدات وثقافات شعبية عريقة (انظر المرجعين (1) و(2)). ومن الرسومات الشهيرة ما يعرف ب«سلحفاة فانواتو» التي تكشف عن فن متميز في المنطقة اتجه في الأخير نحو التجريد والتعقيد والمزيد من التناظر في الأشكال.
كما درس جرديس أيضا رسومات في أنغولا جاءت كما هو موضح في الشكل أدناه وسميت «الديك الهارب». وربط الباحث عدد النقاط داخل الأشكال بعدد الأعمدة وعدد المنحنيات فاستخلص من ذلك خواص رياضية كثيرة لهذه الأشكال تكشف عن عمق إدراك صاحبها لبعض المفاهيم الرياضية. والسؤال الذي يطرحه الدارس في مثل هذه الوضعيات: هل الرسام كان على دراية بتلك العلاقات الرياضية التي نكتبها اليوم بشكل آخر ونعبر عنها برموز الرياضيات الحديثة؟ أو أنها كامنة في الثقافة الشعبية لهؤلاء السكان؟ ومهما يكن الأمر فإن الأجوبة عن مثل هذه الأسئلة تظل غير وافية.
ومن بين ما تضم الثقافة الشعبية في إفريقيا بوجه خاص فن العرافة وقراءة البخت. وقد خصصت دراسات متعددة لهذا الفن من الزاوية الإثنورياضية لا سيما في مدغشقر. ومن المعلوم أن هذا الفن ارتبط في هذه المنطقة بنوع من التنجيم الموروث من البلاد العربية. وقد ورد ذكرها في مخطوطات يرجع تاريخها إلى القرون الوسطى كتبت بالعربية واللاتينية. وامتدت إلى عديد البلدان الإفريقية حتى وصلت إلى تشاد (انظر المرجعين (8) و(12)). والمطلع على هذه الدراسات يكتشف أن هذا الفن مزج بين التاريخ والأثنوغرافيا والرياضيات.
تعتمد قراءة البخت على تقنية خلط نوى نوع من التمر الهندي، وخلال العملية تُقرأ بعض العبارات. ثم تؤخذ كمشة من النوى وتُوضع على الأرض ثم تُؤخذ منه النوى بعدد شفعي (أي 2 أو 4 أو 6 ...) إلى أن تبقى منها نواة واحدة أو اثنتان. وبعد ذلك نكرر العملية 16 مرة. وفي كل مرة يوضع الباقي داخل مصفوفة في شكل جدول (انظر الشكل أدناه).
ونتيجة لهذا السحب العشوائي المتكرر يتحدد مصير السائل. لقد قام الباحثون بدراسة هذا الجدول ونتائجه رياضيا، وتبيّن لهم عدد الجداول الممكنة وخواصها الجبرية. وارتبطت عند البعض بما يعرف بالمربعات السحرية التي انتشرت في الأوساط الشعبية. وقد اتضح أن تشكيلها ليس بالأمر الهين. كان الباحث في تاريخ الرياضيات السويسري جاك سيزيانو Jacques Sesiano قد أسهب في دراسة هذا النوع من المربعات وتاريخها (انظر مثلا المرجع (11)).
في موزنبيق
من المسائل التي تطرحها الإثنورياضيات قضية إبراز الروابط بين الخواص المدروسة من الناحية الرياضية وصلتها بالسياق المعرفي في تلك المجتمعات القبلية، وبصفة خاصة لدى علية القوم فيها. وتتساءل أيضا عن سعة إلمام الأهالي بالرياضيات وعن قواعدها التي تزخر بها ثقافتهم الشعبية.
لقد كرّس الباحث الهولندي الأصلي والموزنبيقي الجنسية باولس جرديس (1952 - 2014) حياته لهذا النوع من الدراسات في إفريقيا، وبصفة خاصة في موزنبيق وأنغولا. وهكذا ألّف في هذا الموضوع قرابة 60 كتابا ونشر أزيد من 100 بحث حول الإثنورياضيات في إفريقيا.
من بين دراسات جرديس دراسة شكل مصيدة من صنع محلي في موزنبيق وخصوصياتها الهندسية.
لاحظ السكان أن هذا الشكل جيد لصيد السمك وغيره. انظر أشكال الفتحات المضلعية السداسية كما هي موضحة في الشكل 1 وكيف يتم نسيجها:
من المعلوم أنه عندما تكون الفتحات سداسية الأضلاع (كما هو مبين في الشكل) فإن الماء يتسرب بسرعة من المصيدة عبر هذه المنافذ. كما لوحظ أن صنع سلات من هذا القبيل لحمل الطيور فيها تكون هي الأنسب لتهوية الطيور ولخفة وزن السلة.
وبهذا الخصوص، يعلم المختصون في الرياضيات أن الأشكال المضلعية المنتظمة السداسية الأضلاع لها خواص لا نجدها في جل الأشكال الأخرى (مقارنة مثلا بتلك التي لها 5 أو 7 أضلاع...). على سبيل المثال، ففي فن التبليط والترصيف تؤدي هذه المضلعات دورا مهما بحيث إذا رُصفت بلاطات من هذا الشكل السداسي فهي لا تترك فراغات بين حوافها (خلافا مثلا للمضلعات الخماسية...). انظر أيضا في هذا الباب إلى شكل بيوت النحل وقارن شكلها بهذه المضلعات.
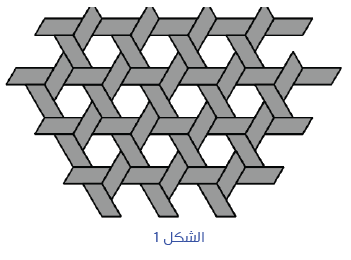

وقد اهتم السكان أيضا بعد ذلك بالمادة النباتية التي يصنعون منها هذه المصيدة وبسعة الفتحات الأنسب وبحجم المصيدة، وبالزوايا المناسبة بين الاتجاهات، إلخ. ما من شك أن هذا الإرث الشعبي انتقل في البلاد الإفريقية أبا عن جد، وبهذا الصدد يتساءل المختصون: كيف يمكن توظيف هذا الإرث الثقافي العلمي في تدريس الرياضيات بالمنطقة؟
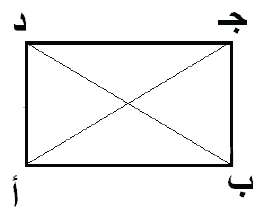
يقدم جرديس مثالين مهمين في الهندسة وكيف يستعملها الفلاحون كنتيجة راسخة في أذهانهم تتوارثها الأجيال عبر ثقافتهم الشعبية. من المعلوم أن الهندسة المألوفة (المسماة الهندسة الإقليدية) تقوم على خمس مسلمات وضعها أقليدس وبنيت عليها كل قواعد الهندسة الإقليدية. لكن المسلمة الخامسة بدت للرياضيين أنه يمكن الاستغناء عنها. وقد أسال موضوعها الكثير من الحبر ولا يزال كذلك لحد الساعة. وكان بعض الرياضيين في النصف الأول من القرن العشرين قد استبدلها بمسلمة أخرى أُطلق عليها «مسلمة المستطيل» (انظر المرجع (7)).
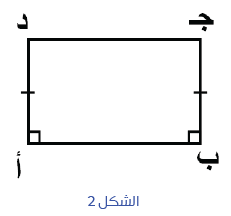
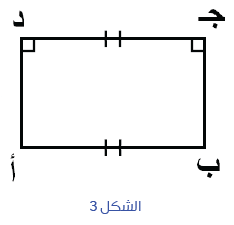
لنوضح نص هذه المسلمة. إذا تساوى في الشكل الرباعي التالي (الشكل 2) الضلعان الشاقوليان (أد = ب ج) مع قيام الزاويتين أ وَ ب فإن لدينا الشكل 3، أي تساوي الضلعين الأفقيين (أب = د ج) مع قيام الزاويتين د وَ ج. وهذا يعني أن الشكل الرباعي مستطيل، أي أن زواياه كلها قائمة، وأن كل ضلعين متقابلين متساويان، وأن قطريه أج و د ب متساويان ويتقاطعان في منتصفهما.
يوضح جرديس أن موروث الثقافة الشعبية بموزنبيق يبيّن أن السكان المزارعين يستعملون في قراهم هذه المسلمة دون أن يطلقوا عليها اسما. ثم يتساءل: لماذا نتكلم عن المسلمة الخامسة وأقليدس الإغريقي في المدرسة ونعلمها لأطفال موزنبيق ولا نبني معارف هؤلاء عما اكتسبوه من بيئتهم؟
كيف يستعمل الموزنبيقيون هذه المسلمة دون أن يدروا: إذا أرادوا بناء منزل فهم يبدأون بوضع الأساس، أي برسم مستطيل على الأرض ذي 4 زوايا قائمة في المكان المناسب. ولهذا الغرض يستعملون طريقتين:
الطريقة الأولى:
يُحضرون أولا قضيبين من الخشب المحلي لهما نفس الطول (طول المنزل الذي يريدون إقامته):
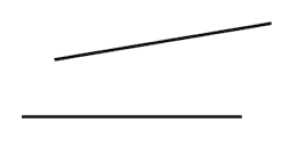
ثم يُحضرون قضيبين آخرين لهما نفس الطول (هذا الطول هو عرض المنزل المراد تشييده) ويجمعون تلك القضبان لتكوّن شكلا رباعيا:
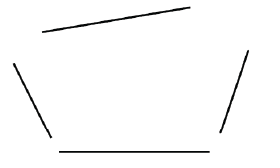
حتى يأخذ الشكل التالي تقريبا:

ثم يصلون الزاويتين أ و ج بحبل وكذلك الزاويتين ب و د بحبل ثان، ويحركون القضبان حتى يتبيّن أن طولي الحبلين أج وَ ب د متساويان (أي تساوي القطرين). وعندئذ نحصل على الشكل المطلوب (قاعدة المنزل المستطيلة الشكل) وهو الشكل التالي:
الطريقة الثانية:
يُحضر صاحب المنزل حبلين متساويي الطول ومربوطين في منتصفهما كما في الشكل:
ثم يُحضر قضيبا بطول عرض المنزل المطلوب تشييده، ويُثبّت طرفاه كما هو مبيّن في الشكل التالي:
أخيرا، نمدد الحبلين أقصى ما يمكن ويُثبت طرفاهما المتبقيان في الأرض فنحصل على الشكل التالي:
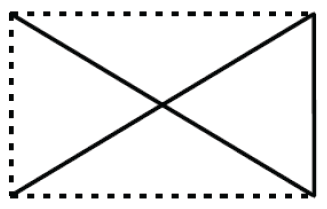
يمثل هذا الشكل فعلا قاعدة المنزل الذي نريد بناؤه.
وهكذا، وبالرجوع إلى القواعد المتبعة في تقاليد البناء بالمنطقة يمكن للتلميذ استيعاب ما توضحه هندسة أقليدس التي تبنى عليها نظريات رياضية كثيرة، كما تفرعت عنها اختصاصات عديدة داخل الرياضيات.
ومن جهة أخرى، درس جرديس الشكل الهندسي للقُمع المحلي المصنوع من قبل الحرفيين في موزنبيق، وكذا الفنيات الهندسية التي يستعملونها والتي تدل على إلمام كبير لهؤلاء بالمفاهيم الهندسية، ولولا مثل هذه الدراسات لاعتقدنا أنهم غافلون عنها تماما. كما استعرض جرديس في مؤلفاته الصناعة الشعبية للسلاّت في جنوب موزنبيق وكيف يتم تصميم غطاء السلة وكيفية غلقها. وبيّن بعد التحليل الهندسي لوضعية السلة أن في ذلك برهانا لنظرية فيثاغورس الشهيرة التي تقدم للتلاميذ في المرحلة الإعدادية. وبطبيعة الحال فصانع السلة لا علم له بهذه النظرية! نشير إلى أن نظرية فيثاغورس عرفت عبر العصور عددا كبيرا من البراهين المختلفة، كما عُممت إلى نظرية أخرى (تعرف باسم نظرية فيرما Fermat المتوفى عام 1665) ظل برهانها مجهولا أزيد من ثلاثة قرون حيث لم يتم البرهان عليها إلا عام 1994 من قِبل البريطاني أندريو وايلز Andrew Wiles.
الإثنورياضيات هنا وهناك
قصة طريفة: دعونا نروي في هذا السياق قصة طريفة لها علاقة بالإثنورياضيات عاشها العلامة الأمريكي ريتشارد فينمان 1918-1988، الحائز على جائزة نوبل في الفيزياء عام 1965 والذي له موهبة خارقة في الحساب الذهني.
يروي فاينمن أنه وخلال زيارة علمية له للبرازيل كان، ذات مرة، يتناول غداءه في أحد المطاعم، ولم يكن هناك زبون غيره في ذلك المطعم. وفجأة دخل رجل آسيوي يظهر عليه من الأميين، يبيع معدادات تقليدية آسيوية، وشرع في استفزاز عمال المطعم قائلا إنه قادر على إجراء عمليات الجمع أسرع من أيّ كان. وللتخلص منه اقترح عليه العمال أن يوجه السؤال لفاينمن (الزبون الوحيد الذي كان في المطعم). فطلب الآسيوي من أحد العمال أن يذكر أية أعداد ليقوم بجمعها بسرعة تفوق سرعة فاينمان. وراح فاينمن والأسيوي يتباريان في جمع تلك الأعداد، كلّ على حدة. لكن الآسيوي كان يستعمل آلته الشعبية التي جاء من أجل بيعها، أما فاينمن فكان يقوم بالحساب ذهنيا بدون أية آلة.
وقد تمكن الآسيوي من التفوق على فاينمن في المرة الأولى والثانية والثالثة ... وشيئا فشيئا كان الفارق الزمني بين الرجلين يتقلّص في الوصول إلى الإجابة الصحيحة. وكان عمال المطعم ينتظرون لحظة فوز فاينمن. وجاءت تلك اللحظة حين أخطأ الآسيوي في حساباته. وحدث ذلك عندما أصبحت العمليات تتطلب استخراج الجذور التكعيبية لبعض الأعداد، إذ لم يكن يدري الرجل الآسيوي أن حظوظه ستتقلص في هذه الحالة لأن آلته التقليدية غير مؤهلة للقيام بذلك.
كان فاينمن يستخرج الجذور التكعيبية ذهنيا دون كتابة بينما كان الآسيوي منهمكا في تحريك كريات آلته، سائلا فاينمن: ماذا تنتظر لبدء الحساب؟! وفوجئ الجميع بدقة نتيجة فاينمن وهزيمة الآسيوي. وبطبيعة الحال، لم يرض الأسيوي بهذه النتيجة النكراء! يروي فاينمن أنه شاهد بعد عدة أسابيع ذلك الأسيوي داخل الفندق الذي يقيم فيه وهو يقوم بعمليات إشهارية لمعداده. فاقترب الأسيوي منه وسأله: كيف استطعت في المرة الماضية أن تقوم بذلك الحساب بسرعة تفوق سرعة الآلة؟
وانطلق فاينمن في شرح طريقته التقريبية: افترض أننا نريد حساب الجذر التكعيبي للعدد 28. إننا نعلم أن الجذر التكعيبي للعدد 27 هو 3. إذن … فقاطعه الآسيوي قائلا: آه، تقول 33´3´=27؟ وسارع إلى معداده للتأكد من ذلك! فأدرك فاينمن أن بائع المعداد لا يعلم شيئا حول الأعداد وخواصها وأن استعمال هذا المعداد لا يستدعي أية معلومات حول العمليات الحسابية المألوفة!
الهندسة الكسورية: لقد تزايد الاهتمام بالإثنورياضيات في بلدان مختلفة خلال السنوات الأخيرة. وركزت البحوث على نشاطات متنوعة: هناك الفنون المرئية (البصرية) التي تميزت بثراء التقاليد وبطرق التزيين والتجميل في عديد المناطق عبر العالم. وقد برز ذلك في الأشكال الهندسية المبنية في أغلب الأحيان على ما يعرف في الرياضيات - وحتى في اللغة الشعبية - بالتناظر أو تداخل المنحنيات والرسومات. ويحاول الباحثون في الأثنورياضيات تفسير ذلك باستخدام المفاهيم الرياضية ومعالجتها بربطها بالثقافة الشعبية.
نشير إلى أن ثمة في الرياضيات ما يسمى بالهندسة الكسورية. وهي فرع من فروع الرياضيات ظهر خلال السبعينيات من القرن العشرين أسسه العالم الفرنسي بينوا مندلبروت Benoît Mandelbrot. وقد لاحظ الباحثون أن هذا الفرع يندرج ضمن الاهتمامات الأنثروبولوجية. وتتميز الهندسة الكسورية بأشكال مبهرة في الجمال والتنوع يرسمها الحاسوب بمجرد تزويده ببعض المعطيات الرياضية البسيطة. والغريب أن منها ما يرجعنا إلى ما نجده في الثقافة الشعبية في فن الرسم ذي الطابع الهندسي (التناظري). ويحاول الباحثون في هذا السياق التعرف على الأشكال الموجودة في الرسومات الفنية لدى المجتمعات البدائية والتي لها صلة بالهندسة الكسورية الحديثة العهد. إليك نموذج من هذه الصور الكسورية التي رسمها الحاسوب:
في سويسرا: تعتبر الرياضيات في المناهج الدراسية السويسرية كثقافة قائمة بذاتها تمثل منهج تفكير ولغة معينة وسبل معالجة الخطأ والصواب. كما أن اكتساب هذه الثقافة تتجاوز مرحلة الإلمام بتقنيات وأدوات أساسية في مجال الحساب أو الهندسة. وإذا كان الأمر كذلك فما المانع أن تُدرج الرياضيات المرتبطة بخصوصيات ثقافات الشعوب المختلفة في المناهج الدراسية؟ ذلك هو السؤال الذي يطرحه المختصون.
ويرى الخبراء أن التلميذ عندما يدخل المدرسة يكون قد ألمّ بالكثير من المعلومات حول كيفية العد والحساب والمقارنة بين الكميات وحل بعض المسائل الحسابية. وكل هذه الأمور يتعلمها الطفل من بيئته، أي من ثقافة والديه ومحيطهما، فإن كان مجتمعه من المجتمعات الإثنية فإن الانطلاق في المدرسة من المفاهيم الإثنورياضية المنبثقة من الثقافة الشعبية أمر جميل ولا شك سيساعد التلميذ على الرقي بفكره. أما إذا انتسب التلميذ إلى مجتمع غربي كما نعرفه اليوم فالأمر يختلف. والواقع أن المناهج في الدول الغربية تشمل العديد من الأمثلة المستقاة من الحضارات الإنسانية الكبيرة مثل الحضارات البابلية والمصرية والإغريقية واللاتينية والصينية... غير أنه لا تتم الإشارة في هذا السياق إلى أية ثقافات شفوية مثل الثقافة الشعبية الإفريقية إلا بصفة محتشمة. وعلى سبيل المثال، نجد في المدرسة السويسرية إشارة إلى المعدادات والعد بالأصابع. وقد ركزت بعض الدراسات على ما سماه بعض الباحثين «الصدمات الإثنورياضياتية».
في فلسطين: بعيدا عن سويسرا، صدر خلال هذا العام كتاب من 316 صفحة حول الإثنورياضيات لدى بدو صحراء النقب في فلسطين. وتناول في فصوله الثلاثة الأولى حياة السكان وتاريخهم العريق وعاداتهم المختلفة. وبعد أن عرّف بالأثنورياضيات ودورها الإيجابي في تدريس الرياضيات تناول في الفصول الأربعة الموالية فن التطريز في مختلف المنسوجات في صحراء النقب وتاريخه ونماذجه وعلاقته بالأشكال الهندسية.
وفي الفصول الثلاثة الأخيرة أثبت المؤلفان أن الإثنورياضيات حاضرة لدى البدو في كل مكان وفي جميع مرافق حياتهم ونشاطاتهم : القياس والقسمة والحياة تحت الخيمة والمفروشات والألبسة وطريقة جلب الماء وحفر الآبار في البادية وكذا في ألعاب التلاميذ. وكل هذا يمكن أن يكون مرتكزا لجعل التلميذ يدرك بسرعة العديد من المفاهيم الرياضية خلال دراسته إذا ما تم توظيف هذه الأدوات بالشكل المناسب. وقد أشار الكاتبان إلى محاولات ناجحة في هذا الاتجاه، لكنها لا زالت في بداياتها (انظر المرجع (10)).
الإثنوحوسبة: من بين الدراسات الحديثة تلك التي انبثقت من المصطلح الإثنوحوسبة ethnocomputing الذي أدخله عام 2002 الباحث الفنلندي ماتي تيدر Matti Tedre في أطروحته (انظر المرجع [14]). والمصطلح يعبر عن التفاعلات بين أجهزة الكمبيوتر والمعرفة الثقافية، منها الثقافة الشعبية.
الخاتمة
نحن بحاجة على مستوى القارات الخمس إلى عصرنة الموارد التي تأتينا بالتراث الثقافي ذي الطابع العلمي. ولا يستثني ذلك مثلا السكان الأصليين الذين يعيشون في أراضي القطب الشمالي لمعرفة استراتيجياتهم من أجل البقاء والتفوق. كيف يمكن لهؤلاء التعامل مع البيئة الطبيعية والاجتماعية والثقافية؟ إنها تساؤلات ومعلومات يمكن أن يستفيد منها التلميذ في أي مكان في العالم إذا ما أحسن توظيفها في مجال التعلم (انظر المرجع (11)).
ينبغي ألا ننسى المعلم في هذا الباب. هناك مشكل يراه الباحثون والداعون إلى توظيف التراث الشعبي في تدريس الرياضيات وهو كيف نكوّن المعلم ليؤدي دوره على أحسن وجه. فالمعلم لا بد أن يتأمل في المحيط الذي يعمل فيه، ويتعين عليه محاولة إيجاد ما يفيد في هذا الموضوع لأن لكل منطقة، وربما لكل بلدة، خصوصيات بعضها يختلف عن جيرانها خاصة في المجتمعات القبلية.
لقد تزايد الاهتمام والبحث في حقل الإثنورياضيات ولم يعد منحصرا على بعض البلدان. تفيد الإحصائيات أن عدد الأطروحات في هذا المجال تجاوز في البرازيل حتى العام الجاري 150 أطروحة دكتوراه وماستر. كما بلغ 50 أطروحة في موزنبيق، ونحو 100 بين الولايات المتحدة ونيوزلندا. وهذا بالإضافة إلى المئات من الأبحاث والإسهامات في المؤتمرات العالمية. إنها أعمال مشجعة تدفع إلى المزيد من الاهتمام بهذا الجانب المعرفي الذي يسعى إلى تقريب الثقافة الشعبية ذات الطابع العلمي من المدرسة في كل مكان.
المراجع
1 Ascher M. : Ethnomathematics: a multicultural view of mathematical ideas, Pacific Grove Ca., Brooks & Cole, 1991.
2 Ascher M.: Mathématiques d’ailleurs : nombres, formes et jeux dans les sociétés traditionnelles. Editions du Seuil, 1998.
3 Borba M. : Etnomatemática: o Homem também conhece o Mundo de um ponto de vista matemático, Bolema, Rio Claro, 3, 5, 1988.
4 Chemillier M.: Les mathématiques naturelles. Paris, Odile Jacob, 2007.
5 Ferreira E. S. : Etnociência: uma metodologia de ensino, Aprender a ensinar, Boletim de Educação Matemática, São Paulo, 2, 1986.
6 D’Ambrosio U. : Reflections on ethnomathematics, ISGEm-Newsletter, Albuquerque, 3, 1, 1987.
7 Gerdes P. & Djebbar A. : Mathematics In African History And Cultures: An annotated Bibliography, African Mathematical Union, Commission on the History of Mathematics in Africa, Cape Town, South Africa, 2007.
8 Jaulin R. : La géomancie. Analyse formelle, Notes mathématiques de R. Ferry et F. Dejean, Cahiers de l’homme, Mouton, Paris, 1966.
9 Kane E. A. : Les systèmes de numération parlée des groupes ouest-atlantiques et Mande. Contribution à la recherche sur les fondements et l’histoire de la pensée logique et mathématique en Afrique de l’Ouest; Lille, 1987.
10 Katsap A. & Silverman F. L. : Ethnomathematics of Negev Bedouins’ Existence in forms, symbols and geometric patterns, Sense Publishers, 2016.
11 Rosa M. et al. : Current and future perspectives of ethnomathematics as a Program ICME-13 Topical Surveys, Springer, 2016.
12 Sadi R. : Configurations et probabilités d'occurrence de la figure unité en P15 en géomancie additive et en géomancie multiplicative, R. Jaulin, Géomancie et Islam, Christian Bourgois, Paris, 1989.
13 Sesiano J. : Un traité médiéval sur les carrés magiques, Lausanne, Presse Polytechniques et Universitaires Romandes, 1996.
14 Tedre, M. : Ethnocomputing; A multicultural view on computer science, University of Joensuu Press, Finland, 2002.
15 Traoré K. : La problématique d’une voie africaine en didactique des mathématiques : vrais et faux enjeux, Revue africaine de didactique des sciences et des mathématiques, 2, 2007.
16 Traoré, K. : Raisonnements sous-jacents à la construction des cases rectangulaires par des paysans Siamous au Burkina Faso. Actes du colloque du Groupe des Didacticiens des Mathématiques du Québec, 2006.
الصور
1 http://wallpaperswide.com/numbers-wallpapers.html
2 http://www.apalconnect.org/wp-conte nt/gallery/cny2016/AbacusLessons.jpg
3 https://wallpaperscraft.com/image/light_moon_fractals_77191_3840x2160.jpg
4 https://beebee225.files.wordpress.com /2014/05/20140218-155846.jpg


































































